今日のお題:行列の積の応用
今回は、前回の続きとして行列の積の応用から始めます。
行列の積を計算したいときは、左側の行(横の並び)の要素数(列の数)と、
右側の列(縦の並び)の要素数(行の数)が等しくなければ、行列の掛け算は
出来ません。逆に言えば、ここが一致すれば、縦横の数の違う行列同士でも
積は作れます。
$$\left(
\begin{array}{ccc}
a_1 & a_2 & a_3 \\
b_1 & b_2 & b_3 \\
\end{array}
\right)\\×\left(
\begin{array}{ccc}
c_1 & d_1 \\
c_2 & d_2 \\
c_3 & d_3
\end{array}
\right)\\=\left(
\begin{array}{ccc}
a_1c_1+a_2c_2+a_3c_3 & a_1d_1+a_2d_2+a_3d_3 \\
b_1c_1+b_2c_2+b_3c_3 & b_1d_1+b_2d_2+b_3d_3 \\
\end{array}
\right)\\$$

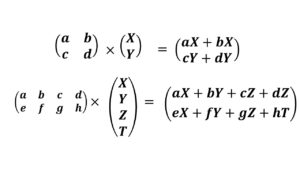
行列を一つの記号A等で表すことが多い。
また、間のXは省略が多い。
行列の積では必ずしも交換法則は成り立たない。(成り立つこともある。)
AB≠BA(交換法則が成り立たない場合)
行列はAとBを入れ替えると2×3、3×2のように同じにならないこと。
それを証明してみましょう。
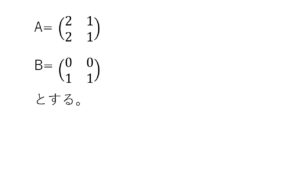
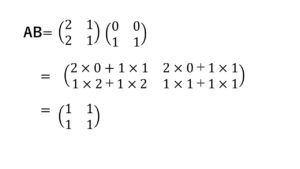
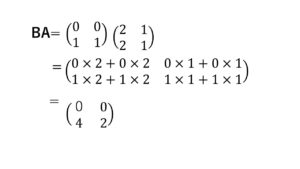
このように成り立たないことが証明されました。
(交換法則が成り立つ場合)
今度は、交換法則が成り立つ場合をみていきましょう。
(ⅰ)ある行列Aと単位行列E、例行列Oは交換可能
単位行列E、例行列Oは後で説明します。
(ⅰ)AE=EA
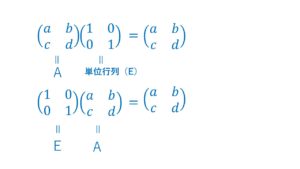
(ⅱ)AO=OA
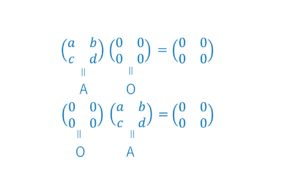
(ⅱ)ある行列のべき乗A同士の積
(ⅱ)AA²=A²A
一つの行列のべき乗は交換可能
(ⅲ)対角行列と対角行列は交換可能
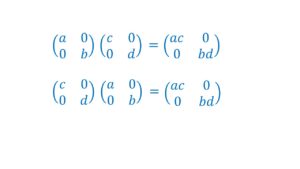
対角行列についても後で説明します。
(ⅰ)~(ⅲ)のように特別として成り立つこともあります。
今回も長くなってしまったのでここまでにします。
続きは次回にします。