今日のお題:行列について
今回は、行列式の計算の仕方について紹介していきます。
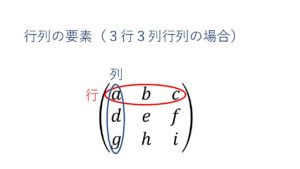
行列とは?
数学における行列とは、ある程度を縦横に並べたものです。
横を行と呼び、縦方向を列と呼びます。
行列の計算の仕方
$$A = \left(
\begin{array}{ccc}
1 & 2 \\
3 & 4 \\
\end{array}
\right)\\B = \left(
\begin{array}{ccc}
5 & 6 \\
7 & 8 \\
\end{array}
\right)\\とする。$$
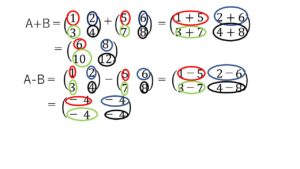
行列の和と積は、必ず対応する位置の加減となります。
従って、行列と列数の一致する行列同士でないと足し算、引き算は
出来ません。
行列全体に一つの数をかけられる。
これをスカラー倍といいます。
$$A×\begin{pmatrix} 1&3 \\ 2 & 4 \end{pmatrix}=\begin{pmatrix} A & 3A \\ 2A & 4A \end{pmatrix}$$
今度は複雑な計算式となる行列の積についてみていきましょう。
左側は行(横の並び)、右側は列(縦の並び)に着目します。
そして、それぞれの組の順番同士でかけあわせたものを足していきます。
$$例えば\begin{pmatrix} a&c \\ b & d \end{pmatrix}×\begin{pmatrix} e& f \\g & h \end{pmatrix}=\begin{pmatrix} ae+bg&af+bh\\ ce+dg & cf+dh \end{pmatrix}$$
となりますがそうなる理由を順にみていきましょう。
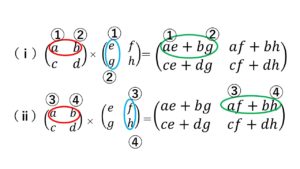
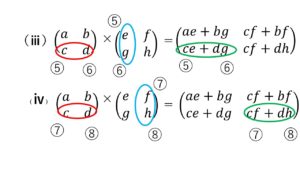
このように番号で振り分けた順に計算します。
長くなるので今回はこれで終わりにします。